How Many Sides Does a Polygon Have? Unveil the Mystery!

A polygon has multiple sides. The number of sides varies depending on the shape.
Have you ever wondered how many sides a polygon has? The answer is simple – a polygon is a closed shape with three or more sides. From triangles with three sides to polygons with countless sides, these shapes are found everywhere in nature and man-made structures.
Understanding the characteristics of polygons can help in various fields, from geometry to architecture. In this blog post, we will explore the fascinating world of polygons, their properties, and real-world applications. Let’s dive in and unravel the mystery of these versatile geometric figures.
Credit: americanboard.org
The Basic Definition Of A Polygon
A polygon is a two-dimensional shape that is formed by straight lines and is closed. It is a geometric figure that consists of a finite number of line segments connected end to end to form a closed shape.
Characteristics Of Polygons
Polygons have several defining characteristics:
- Straight sides: All sides of a polygon are straight lines.
- Closed shape: A polygon is a closed figure, which means that it has no openings.
- Fixed number of sides: A polygon has a specific number of sides, with a minimum of three.
- Interior angles: The interior angles of a polygon add up to a specific value, which varies based on the number of sides.
- No intersecting sides: The sides of a polygon do not intersect with each other.
Polygons Versus Non-polygons
The distinction between polygons and non-polygons is clear:
| Polygons | Non-Polygons |
|---|---|
| Have straight sides | May have curved sides |
| Are closed shapes | Can be open shapes |
| Have a fixed number of sides | Can have an indefinite number of sides |
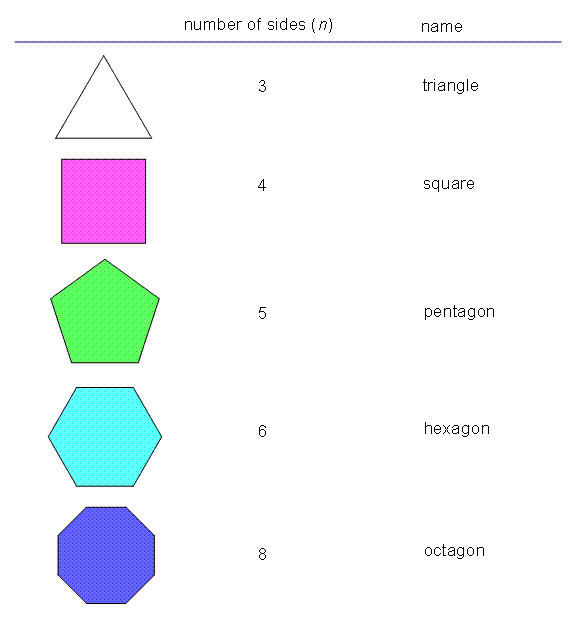
Classifying Polygons By Sides
Discovering the number of sides in a polygon involves classifying them based on their unique characteristics and shapes. Polygons can have varying numbers of sides, with common examples being triangles, quadrilaterals, pentagons, and hexagons. Understanding these distinctions helps in identifying and working with different types of polygons effectively.
Classifying Polygons by Sides When we talk about polygons, we are referring to closed figures with three or more straight sides. Polygons can have varying numbers of sides, and it is essential to classify them based on the number of sides they have. We can classify polygons into different categories, including triangles, quadrilaterals, and polygons with more than four sides. Below, we will discuss these categories in more detail.
Triangles: The Simplest Polygons
Triangles are the simplest polygons as they have only three sides. There are different types of triangles, including equilateral, isosceles, and scalene triangles. An equilateral triangle has three equal sides, while an isosceles triangle has two equal sides. A scalene triangle has no equal sides. Triangles are fundamental shapes, and they play a crucial role in the field of geometry.
Quadrilaterals And Beyond
Quadrilaterals are polygons with four sides, and they come in different shapes, including squares, rectangles, rhombuses, and trapezoids. A square has four equal sides and four right angles, while a rectangle has four right angles but not necessarily equal sides. A rhombus has four equal sides but no right angles, while a trapezoid has one pair of parallel sides. Polygons with more than four sides include pentagons, hexagons, heptagons, octagons, and nonagons. A pentagon has five sides, a hexagon has six sides, a heptagon has seven sides, an octagon has eight sides, and a nonagon has nine sides. These polygons also have unique properties and characteristics, making them essential in geometry.
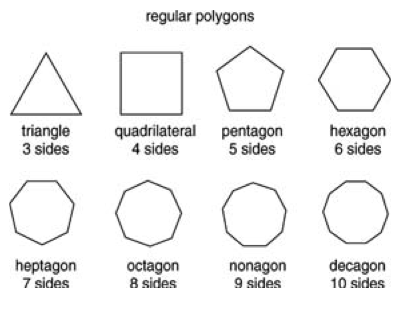
Naming Polygons Up To 12 Sides
We can also name polygons based on the number of sides they have. For instance, a polygon with ten sides is known as a decagon, while one with twelve sides is called a dodecagon. Naming polygons makes it easier to classify them and study their properties. Below is a table showing the names of polygons up to twelve sides.
| Number of Sides | Name of Polygon |
|---|---|
| 3 | Triangle |
| 4 | Quadrilateral |
| 5 | Pentagon |
| 6 | Hexagon |
| 7 | Heptagon |
| 8 | Octagon |
| 9 | Nonagon |
| 10 | Decagon |
| 11 | Hendecagon |
| 12 | Dodecagon |
In conclusion, classifying polygons based on the number of sides they have is essential in the field of geometry. It enables us to understand their properties and characteristics, making it easier to study them. From triangles to polygons with twelve sides, each category has unique properties that make them stand out.
The Infinite Possibility Of Sides
Explore the endless world of polygons and their sides. Uncover the answer to the intriguing question: how many sides does a polygon have? Delve into the fascinating realm of geometry and discover the infinite possibilities that lie within these multifaceted shapes.
Beyond Dodecagons
A polygon is a geometric shape that consists of straight lines connected to form a closed figure. While most of us are familiar with common polygons like triangles, rectangles, and pentagons, the possibilities for the number of sides in a polygon are practically infinite. Beyond the well-known shapes, there exists a vast world of polygons with varying numbers of sides, each with its unique properties and characteristics.
One notable example is the dodecagon, a polygon with twelve sides. Its symmetrical structure and equal angles make it a popular choice in design and architecture. However, the exploration of polygons doesn’t stop at twelve sides. In fact, mathematicians have discovered polygons with hundreds, thousands, and even millions of sides.
The concept of polygons with a large number of sides might seem abstract or even incomprehensible at first. After all, how can we visualize a shape with thousands of sides? To better understand this, let’s consider the idea of a regular polygon, where all sides and angles are equal.
Imagine a regular polygon with a high number of sides, such as a thousand. As the number of sides increases, the polygon starts to resemble a circle more closely. In fact, as the number of sides approaches infinity, the polygon becomes indistinguishable from a circle. This fascinating connection between polygons and circles showcases the infinite potential of polygons.
When Does A Polygon Stop Being A Polygon?
While the possibilities for the number of sides in a polygon are limitless, there is a point where a shape stops being considered a polygon. To be classified as a polygon, a shape must meet certain criteria:
- The shape must be two-dimensional, lying on a flat plane.
- It must consist of straight lines.
- The lines must be connected to form a closed figure.
- Each line must intersect exactly two other lines, with no intersecting lines within the shape.
When any of these criteria are not met, the shape is no longer considered a polygon. For example, a curved line or a shape with intersecting lines would not be classified as a polygon. The definition of a polygon provides a clear boundary for what can be considered a polygon and what cannot.
Understanding the infinite possibility of sides in a polygon and the criteria for classification allows us to explore the diverse world of geometric shapes. By expanding our knowledge of polygons, we gain a deeper appreciation for the intricacies of mathematics and the beauty found in the seemingly simplest of shapes.
Regular Vs. Irregular Polygons
When it comes to polygons, they can be classified into two main categories: regular and irregular. Regular polygons have equal sides and equal angles, while irregular polygons have sides and angles of varying lengths and measures. Let’s explore the characteristics of these two types of polygons in more detail.
Equilateral And Equiangular Regularity
Regular polygons are known for their symmetry and uniformity. One type of regular polygon is the equilateral polygon, where all sides are of equal length. An equilateral triangle is a prime example, with all three sides measuring the same. Other examples include the square, with four equal sides, and the regular pentagon, with five equal sides.
Equiangular regular polygons, on the other hand, have equal angles. Each interior angle in these polygons is the same. The equilateral triangle is also equiangular, with each angle measuring 60 degrees. The square is another equiangular regular polygon, with all angles measuring 90 degrees. Regular hexagons, octagons, and other polygons can also fall into this category.
The Diversity Of Irregular Shapes
Irregular polygons, as the name suggests, lack the uniformity found in regular polygons. These shapes can have sides of different lengths and angles of varying measures. The irregularity of these polygons leads to a vast array of shapes and sizes.
Some examples of irregular polygons include trapezoids, which have one pair of parallel sides, and parallelograms, which have opposite sides that are parallel and equal in length. Quadrilaterals such as rectangles and rhombuses can also be considered irregular polygons due to their varying angles.
Irregular polygons offer endless possibilities in terms of shape and design. Their unique characteristics allow for more creativity and flexibility in various applications, from architecture to art.
| Regular Polygons | Irregular Polygons |
|---|---|
| Equilateral Triangle | Trapezoid |
| Square | Parallelogram |
| Regular Pentagon | Rectangle |
| Regular Hexagon | Rhombus |
Understanding the distinction between regular and irregular polygons is essential in geometry and various real-world applications. Regular polygons possess a sense of order and symmetry, while irregular polygons offer versatility and unique design possibilities.
The Role Of Angles In Polygons
Polygons are fascinating geometric shapes that are all around us. Understanding the angles within polygons is crucial to understanding their properties and characteristics. Let’s delve into the role of angles in polygons and explore the Interior Angle Sum Property and the secrets of Exterior Angles.
Interior Angle Sum Property
In a polygon, the sum of its interior angles can be determined using a simple formula. For a polygon with n sides, the sum of its interior angles is equal to (n-2) 180 degrees. This property is essential in calculating individual interior angles and understanding the overall structure of polygons.
Exterior Angles And Their Secrets
The exterior angles of a polygon play a crucial role in understanding its overall shape and characteristics. Each exterior angle is supplementary to the interior angle adjacent to it. This means that the sum of each exterior angle and its corresponding interior angle is always 180 degrees. Understanding the secrets of exterior angles provides valuable insights into the symmetry and properties of polygons.
Mathematical Formulas Involving Polygons
Calculating The Sum Of Interior Angles
A polygon is a closed shape with straight sides. The sum of interior angles in a polygon can be calculated using the formula: Sum = (n – 2) 180° where n represents the number of sides.
Finding The Number Of Diagonals
The number of diagonals in a polygon can be found using the formula: Diagonals = n (n – 3) / 2 where n is the number of sides.
Polygons In The Real World
Exploring the fascinating world of polygons reveals their omnipresence in various aspects of our lives. From architectural marvels to nature’s geometric preferences, polygons play a vital role in shaping our surroundings and natural environment.
Architectural Marvels
In architecture, polygons are fundamental in creating iconic structures. Skyscrapers, bridges, and domes often incorporate polygons to achieve stability and aesthetic appeal.
Nature’s Geometric Preferences
Nature showcases polygons in intricate patterns of leaves, snowflakes, and beehives. The symmetry and efficiency of these natural formations highlight the beauty and functionality of polygons in the real world.
Credit: socratic.org
Exploring Polygons Through Technology
Embark on a journey to explore the world of polygons using innovative technology. Discover the answer to the intriguing question: “How many sides does a polygon have? ” Engage in interactive learning experiences to gain a deeper understanding of polygonal shapes.
Computer Graphics And Polygons
Polygons play a crucial role in computer graphics.
The Role Of Polygons In 3d Modeling
Polygons serve as building blocks in 3D modeling. Polygons are used to create realistic 3D objects. In 3D models, polygons define the shape and surface. They are essential for rendering intricate structures. Polygons are fundamental elements in virtual environments. Polygons are the foundation of digital imagery. Computer graphics heavily rely on polygon manipulation. By understanding polygons, we enhance digital creativity. Polygons drive advancements in animation and design. Technology continues to push the boundaries of polygon usage.

Credit: www.flickr.com
Frequently Asked Questions
How Many Sides Does A Polygon Have?
A polygon can have any number of sides, as long as it has at least three sides. The number of sides in a polygon determines its shape and name. For example, a triangle has three sides, a quadrilateral has four sides, and a pentagon has five sides.
The more sides a polygon has, the more complex its shape becomes.
What Is The Minimum Number Of Sides A Polygon Can Have?
The minimum number of sides a polygon can have is three. A polygon with three sides is called a triangle. Triangles are the simplest form of polygons and are made up of three line segments connected end to end. Triangles come in different types, such as equilateral, isosceles, and scalene, depending on the lengths of their sides.
Can A Polygon Have An Infinite Number Of Sides?
No, a polygon cannot have an infinite number of sides. By definition, a polygon is a closed figure with straight sides. In order for a shape to have straight sides, it must have a finite number of sides. If a shape had an infinite number of sides, it would form a circle rather than a polygon.
Conclusion
Polygons are closed shapes with straight sides and angles. The number of sides depends on the type of polygon, ranging from three in a triangle to infinity in a circle. Understanding the properties of polygons is crucial in various fields, including architecture, engineering, and mathematics.
With this knowledge, you can identify and classify different shapes and use them in practical applications. Keep exploring the fascinating world of polygons and their properties.



