How Many Triangles? Unravel the Mystery Now!

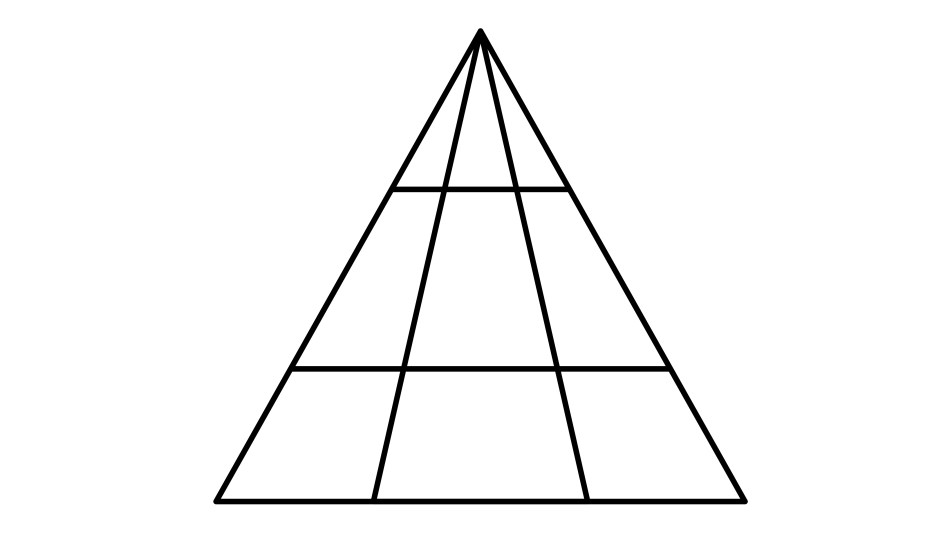
There are 18 triangles. Count carefully to ensure you don’t miss any.
Triangles are a common shape that appears in various contexts, from geometry to art and design. Understanding the number of triangles within a given figure can be a fun and challenging exercise. By accurately counting and identifying these shapes, you can enhance your spatial awareness and problem-solving skills.
In this blog, we will delve into the intriguing world of triangles, exploring their significance and applications across different fields. Whether you are a math enthusiast, an artist, or simply curious about shapes, this exploration of triangles will surely pique your interest. So, let’s begin our journey into the fascinating realm of triangles and uncover the hidden patterns within!
The Fascination With Triangles
Unraveling the mystery of counting triangles is a captivating endeavor. Discovering the numerous ways to count the triangles within a larger triangle provides a stimulating challenge. Engaging in this activity fosters a deeper appreciation for the intricate nature of geometric shapes.
Triangles have fascinated human beings for centuries. They are simple yet complex shapes that have captured the attention of mathematicians, scientists, and artists alike. From the ancient Egyptians to modern-day architects, the triangle has played a significant role in human history. In this blog post, we will explore the cultural significance and mathematical importance of triangles.
Cultural Significance
Triangles have held cultural significance throughout history. In ancient Egypt, triangles represented the trinity of the gods and were used in architectural designs. In Christianity, the triangle is often used to represent the Holy Trinity. In Hinduism, the triangle is used to represent the divine power of the feminine energy. The triangle has also been used in art to represent stability and balance.
Mathematical Importance
The triangle is a fundamental shape in geometry and plays an important role in mathematics. The Pythagorean theorem, which states that the sum of the squares of the two shorter sides of a right triangle is equal to the square of the hypotenuse, is one of the most famous mathematical concepts involving triangles. Triangles are also used in trigonometry to calculate the relationships between angles and sides of triangles. Triangles are also important in computer graphics, where they are used to create 3D models. They are also used in engineering and architecture to design structures, such as bridges and buildings. In conclusion, the fascination with triangles is not limited to just mathematics or culture, but it extends to various fields of study. The simple yet complex shape of the triangle has proven to be an important element in human history and continues to be a vital component in modern-day applications.
Starting With The Basics
Discover the fascinating world of triangles and learn how to count them efficiently. From the basic principles to advanced techniques, this blog post provides a clear and concise guide to mastering triangle counting. Gain a deeper understanding of geometry and enhance your problem-solving skills in a fun and engaging way.
Defining A Triangle
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry and is formed by connecting three non-collinear points. The three sides of a triangle can be of varying lengths, and the angles between them can also differ. The sum of the three angles in a triangle always adds up to 180 degrees.
Types Of Triangles
There are three main types of triangles: equilateral, isosceles, and scalene. An equilateral triangle has all three sides of equal length and all three angles of equal measure (60 degrees). An isosceles triangle has two sides of equal length and two angles of equal measure. A scalene triangle has all three sides of different lengths and all three angles of different measures. Aside from these three types, there are also right triangles, which have one angle measuring 90 degrees. Right triangles can be further classified as either acute or obtuse, depending on the measures of their other two angles. Acute triangles have two acute angles (less than 90 degrees), while obtuse triangles have one obtuse angle (greater than 90 degrees). Knowing the different types of triangles is important in geometry as it helps in identifying properties unique to each type. For instance, equilateral triangles have the largest area for a given perimeter, while right triangles have special properties related to trigonometric functions. In conclusion, understanding the basics of triangles and their types is essential in geometry. It is the foundation for more complex concepts, such as trigonometry and calculus.
Triangle Counting Puzzles
Triangle counting puzzles have gained immense popularity as brain teasers that challenge our problem-solving skills. These puzzles require us to count the number of triangles within a given figure, often deceiving us with their intricate designs. Let’s explore the popularity of these brain teasers and some examples of triangle puzzles.
Popularity Of Brain Teasers
Brain teasers have always intrigued people of all ages. They offer a fun and engaging way to exercise our minds and improve cognitive abilities. Triangle counting puzzles, in particular, have become quite popular due to their visual appeal and the mental challenge they present. These puzzles can be found in puzzle books, online platforms, and even in educational settings.
Examples Of Triangle Puzzles
Triangle puzzles come in various forms and difficulty levels. Let’s take a look at a few examples:
- Simple Figures: These puzzles involve straightforward figures with a few triangles. Counting the triangles correctly can be a good warm-up exercise.
- Complex Designs: These puzzles feature intricate designs that require careful observation and analysis. They often involve overlapping triangles, making the counting process more challenging.
- Geometric Patterns: Some triangle puzzles are based on specific geometric patterns, such as concentric triangles or symmetrical arrangements. These puzzles test our ability to identify patterns and apply mathematical concepts.
By engaging in triangle counting puzzles, we not only enhance our problem-solving skills but also develop patience, attention to detail, and critical thinking abilities. These brain teasers offer an enjoyable way to stimulate our minds and keep them sharp.
Strategies For Solving Triangular Mysteries
Pattern Recognition
Identifying recurring shapes within the triangle.
Geometric Decomposition
Breaking down the triangle into simpler forms for analysis.
Common Pitfalls And How To Avoid Them
When it comes to solving the “How Many Triangles” puzzle, there are a few common pitfalls that many people fall into. These pitfalls can lead to incorrect answers or unnecessary confusion. In order to help you avoid these pitfalls, let’s take a closer look at two of the most common ones: overlapping areas and assumed lines.
Overlapping Areas
One of the main challenges when counting triangles in complex shapes is dealing with overlapping areas. In some cases, triangles can intersect or share sides, making it difficult to determine the exact number of triangles. To avoid confusion, it’s important to carefully analyze the shape and identify each individual triangle.
Here are a few strategies to help you overcome this challenge:
- Start by identifying the triangles that are clearly defined and not overlapping with any other triangles.
- Next, focus on the overlapping areas and determine if they form additional triangles or if they are part of the existing ones.
- If you encounter a complex overlapping area, try mentally separating the triangles or use a pencil to outline them on paper.
- Take your time and double-check your count to ensure you haven’t missed any triangles.
By following these strategies, you’ll be able to navigate through overlapping areas with ease and accuracy.
Assumed Lines
Another common pitfall in counting triangles is assuming the presence of lines that are not explicitly shown in the puzzle. Sometimes, our minds tend to fill in the gaps and create lines that are not actually there. This can lead to incorrect triangle counts.
To avoid assuming lines, keep the following tips in mind:
- Stick to what is clearly shown in the puzzle and avoid adding any lines that are not explicitly provided.
- Be cautious of angles that may give the illusion of additional lines or triangles.
- If you’re unsure about the presence of a line, try different interpretations without adding or assuming any lines.
- Remember to count only the triangles that are formed by the given lines and angles.
By being mindful of assumed lines, you’ll be able to accurately count the triangles without introducing any unnecessary elements.
The Role Of Symmetry
The Role of Symmetry plays a crucial part in understanding and identifying the number of triangles within a given shape. Symmetry provides a framework for recognizing patterns, which in turn aids in the accurate counting of triangles. Understanding Symmetrical Shapes, Application in Triangle Counting, and the significance of symmetry in this context can shed light on the intricate nature of geometric figures.
Understanding Symmetrical Shapes
Symmetrical shapes possess a balance and harmony that make them visually appealing. They are characterized by a mirror image or rotational symmetry, which allows for the identification of patterns and repetitions within the shape. This symmetry is key to unlocking the secrets of triangle counting, as it enables us to predict and identify the various configurations that triangles can form within the shape.
Application In Triangle Counting
When it comes to counting triangles, symmetry serves as a guiding principle. By recognizing and leveraging the symmetrical properties of a shape, we can systematically identify and count the triangles it contains. Symmetry helps us to avoid overlooking any triangles and ensures a comprehensive and accurate count.
Advanced Techniques In Triangle Detection
Using Graph Theory
Graph theory is applied to identify triangles in networks.
Algorithmic Approaches
Algorithms efficiently determine triangles in large datasets.
Interactive Challenges
Engage with our exciting Online Puzzles and Games to test your triangle counting skills.
Online Puzzles And Games
Challenge yourself with interactive games to count triangles. Have fun while enhancing your visual acuity.
Engaging The Community
Collaborate with others, share strategies, and conquer triangle counting challenges together.
Applying Skills Beyond Puzzles
How Many Triangles is more than just a fun game; it offers valuable learning opportunities that extend beyond solving puzzles. By engaging with this game, players can enhance their cognitive abilities and critical thinking skills.
Educational Benefits
- Improves spatial reasoning and problem-solving skills.
- Enhances mathematical thinking and geometric understanding.
- Boosts attention to detail and concentration levels.
Real-world Applications
- Helps in architectural and engineering design concepts.
- Used in computer graphics and image processing algorithms.
- Applied in analyzing network structures and data visualization.
Credit: www.womansworld.com
Conclusion: Beyond Counting Triangles
Exploring the fascinating world of triangles goes beyond mere counting. Let’s dive into the Summary of Techniques and the importance of Encouraging Mathematical Curiosity.
Summary Of Techniques
Understanding triangles involves various techniques:
- Identifying different types of triangles
- Applying the Pythagorean Theorem
- Using trigonometric functions
- Utilizing geometric formulas
Encouraging Mathematical Curiosity
Encouraging curiosity in math can:
- Lead to deeper understanding
- Foster problem-solving skills
- Promote critical thinking

Credit: www.youtube.com
Frequently Asked Questions
How Many Triangles Can Be Formed?
You can form different types of triangles based on the number of sides and angles. In general, given n points, you can form nC3 triangles. So, for example, if you have 6 points, you can form 6C3 = 20 triangles.
However, not all combinations of points will form valid triangles.
What Are The Properties Of A Triangle?
A triangle is a polygon with three sides and three angles. Some key properties of a triangle include: the sum of its interior angles is always 180 degrees, the sum of the lengths of any two sides is always greater than the length of the third side (Triangle Inequality Theorem), and the longest side is opposite the largest angle (Law of Sines).
How To Count The Number Of Triangles In A Figure?
To count the number of triangles in a figure, start by identifying all the triangles that are clearly visible. Then, look for smaller triangles within larger triangles, counting each one separately. Finally, check for any overlapping triangles and count them as well.
Remember to include both equilateral and isosceles triangles in your count.
Conclusion
Discovering the number of triangles in a complex pattern can be both intriguing and challenging. By understanding the principles and techniques involved, you can enhance your problem-solving skills and logical reasoning. The process of counting triangles can also provide a fun and engaging way to exercise your brain and improve your mental agility.



